Trignometric Waveforms
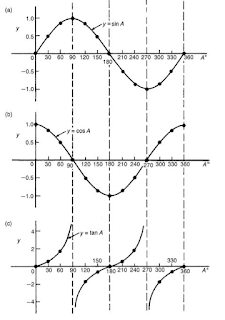
1. Each of the functions below repeat themselves as angle A increases and are thus called perodic functions
2. y = sin A and y = cos A repeat themselves every 360◦; thus 360◦ is called the period of these waveforms. y = sin 2A and y = cos 2A repeat themselves every 180◦ or 𝝅 radians; thus 180◦ is the period of these waveforms
3. In general, if y = sin pA or y = cos pA (where p is a constant) then the period then the period of the waveform is 360◦ /p (or 2π/p rad). Hence if y=sin 3A then the period is 360/3, i.e. 120◦, and if y=cos 4A then the period is 360/4, i.e. 90◦.
Amplitude
Amplitude is the name given to the maximum or peak value of a sine wave.
Lagging and Leading Angles
1. A sine or cosine curve may not always start at 0◦. To show this is a periodic function is represented by y = sin (A∓α) or y = cos (A∓α) where α is a phase displacement compared with y = sin A or y = cos A
Sinusoidal form "A \: sin (\omega t \pm \alpha)")
Let OR represent a vector that is free to rotate anticlockwise about O at a velocity of ⍵ rad/s. A rotating vector is called a phasor. ST = TO sin ⍵t
If the phasor makes one revolution in T seconds, then the angular velocity
⍵ = 2π/T
f = 1/T = number of cycles per second
⍵ = 2πf
Harmonic synthesis with complex waveforms
A waveform that is not sinusoidal is called a complex wave. Harmonic analysis is the process of resolving a complex periodic waveform into a series of sinusoidal components of ascending order of frequency. Many of the waveforms met in practice can be represented by the following mathematical
expression.
u = V1m sin(ωt + α1) + V2m sin(2ωt + α2) + · · ·+Vnm sin(nωt + αn)
the magnitude of their harmonic components together with their phase may be calcuated using Fourier series.
Hyperbolic functions
Functions which are associated with the geometry of the conic section called a hyperbola are
called hyperbolic functions. Applications of hyperbolic functions include transmission line theory and catenary problems.
hyperbolic sine of x
often abbrivated to sh x.. pronounced 'shine x'
hyperbolic cosine of x
often abbrivated to ch x.. pronounced 'kosh x'
often abbrivated to th x.. pronounced 'than x'
Relationship between trigonometric and hyperbolic functions
 "cos\: \theta = \tfrac{1}{2}(e^{i\theta}+e^{-i\theta})")
 "sin\: \theta = \tfrac{1}{2i}(e^{i\theta}-e^{-i\theta})")
 "cos\: i\theta = \tfrac{1}{2}(e^{i*i\: \theta}+e^{-i*i\: \theta})")
 "sin\: i\theta = \tfrac{1}{2i}(e^{i*i\: \theta}-e^{-i*i\: \theta})")
1. Each of the functions below repeat themselves as angle A increases and are thus called perodic functions
2. y = sin A and y = cos A repeat themselves every 360◦; thus 360◦ is called the period of these waveforms. y = sin 2A and y = cos 2A repeat themselves every 180◦ or 𝝅 radians; thus 180◦ is the period of these waveforms
3. In general, if y = sin pA or y = cos pA (where p is a constant) then the period then the period of the waveform is 360◦ /p (or 2π/p rad). Hence if y=sin 3A then the period is 360/3, i.e. 120◦, and if y=cos 4A then the period is 360/4, i.e. 90◦.
Amplitude
Amplitude is the name given to the maximum or peak value of a sine wave.
Lagging and Leading Angles
1. A sine or cosine curve may not always start at 0◦. To show this is a periodic function is represented by y = sin (A∓α) or y = cos (A∓α) where α is a phase displacement compared with y = sin A or y = cos A
Sinusoidal form
Let OR represent a vector that is free to rotate anticlockwise about O at a velocity of ⍵ rad/s. A rotating vector is called a phasor. ST = TO sin ⍵t
If the phasor makes one revolution in T seconds, then the angular velocity
⍵ = 2π/T
f = 1/T = number of cycles per second
⍵ = 2πf
Harmonic synthesis with complex waveforms
A waveform that is not sinusoidal is called a complex wave. Harmonic analysis is the process of resolving a complex periodic waveform into a series of sinusoidal components of ascending order of frequency. Many of the waveforms met in practice can be represented by the following mathematical
expression.
u = V1m sin(ωt + α1) + V2m sin(2ωt + α2) + · · ·+Vnm sin(nωt + αn)
the magnitude of their harmonic components together with their phase may be calcuated using Fourier series.
Hyperbolic functions
Functions which are associated with the geometry of the conic section called a hyperbola are
called hyperbolic functions. Applications of hyperbolic functions include transmission line theory and catenary problems.
hyperbolic sine of x
often abbrivated to sh x.. pronounced 'shine x'
hyperbolic cosine of x
often abbrivated to ch x.. pronounced 'kosh x'
hyperbolic tangent of x
