1) If a² - b² is a prime number, show that a² - b² = a +b, where a and b are natural numbers
a² - b² = (a-b) (a+b)
∵ (a² - b² ) is a prime number
∴ one of the two factors = 1
∵ a -b = 1 [∵ a -b < a + b]
∵ the only divisor of a prime number are 1 and itself
a² - b² = 1 (a +b)
or a² - b² = a + b
example 3² - 2² = 5 (which is a prime)
3² - 2² = 3 + 2, 3,2 𝝐 N
2) Prove that sqaure of each odd number is of the form 8j+1
Let n = 2m + 1 be an odd number
n² = (2m+1)² = 4m² + 4m + 1
= 4m (m+1) + 1
Now m (m+1) being product of two consecutive integers, is divisible by 2! = 2
m(m+1) = 2j
⇒ n² = 4 (2j) +1 = 8j+1
3) Show that sum of an interger and its square is even
Let n be any integer
so, we have to prove that n² + n is even
⇒ n² + n = n (n+1) which is product of two consecutive number n and n+1 and hence divisible by 2! = 2
Hence, n² + n is an even number
4) If n is an integer. Prove that product n( n² - 1 ) is a multiple of 6
n( n² - 1 ) = n(n-1)(n+1) = (n-1) n (n+1)
which being the product of three consecutive integers is divisible by 3! = 6
∴ n (n² - 1 ) is divisible by 6
i.e. n (n² - 1 ) is a multiple of 6
5. Prove 8ⁿ - 3ⁿ is divisible by 5
8ⁿ - 3ⁿ = ( 8 - 3) (8ⁿ⁻¹ + 8ⁿ⁻² . 3 +... 3ⁿ⁻¹)
or 8ⁿ - 3ⁿ = ( 5) (8ⁿ⁻¹ + 8ⁿ⁻² . 3 +... 3ⁿ⁻¹)
∴ 8ⁿ - 3ⁿ is divisible by 5
6. Prove that n⁵ - n is divisible by 5
n⁵ - n = n(n-1)(n+1)(n² + 1)
If the integer n terminates with one of the digits 0, 1, 4, 5, 6, or 9 then one of the first three
is divisible by 5
If n ends in one of the digits 2, 3, 7 or 8 then n² ends in 4 or 9, and in this event n² + 1 is divisible by 5
7. Prove that n⁷ - n is divisible by 7
8. Prove that n¹¹ - n is divisible by 11
9. Prove that n¹³ - n is divisible by 13
10. Prove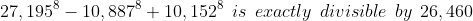
&space;\\*&space;27,195&space;=&space;3.5.7^2.37)
a² - b² = (a-b) (a+b)
∵ (a² - b² ) is a prime number
∴ one of the two factors = 1
∵ a -b = 1 [∵ a -b < a + b]
∵ the only divisor of a prime number are 1 and itself
a² - b² = 1 (a +b)
or a² - b² = a + b
example 3² - 2² = 5 (which is a prime)
3² - 2² = 3 + 2, 3,2 𝝐 N
2) Prove that sqaure of each odd number is of the form 8j+1
Let n = 2m + 1 be an odd number
n² = (2m+1)² = 4m² + 4m + 1
= 4m (m+1) + 1
Now m (m+1) being product of two consecutive integers, is divisible by 2! = 2
m(m+1) = 2j
⇒ n² = 4 (2j) +1 = 8j+1
3) Show that sum of an interger and its square is even
Let n be any integer
so, we have to prove that n² + n is even
⇒ n² + n = n (n+1) which is product of two consecutive number n and n+1 and hence divisible by 2! = 2
Hence, n² + n is an even number
4) If n is an integer. Prove that product n( n² - 1 ) is a multiple of 6
n( n² - 1 ) = n(n-1)(n+1) = (n-1) n (n+1)
which being the product of three consecutive integers is divisible by 3! = 6
∴ n (n² - 1 ) is divisible by 6
i.e. n (n² - 1 ) is a multiple of 6
5. Prove 8ⁿ - 3ⁿ is divisible by 5
8ⁿ - 3ⁿ = ( 8 - 3) (8ⁿ⁻¹ + 8ⁿ⁻² . 3 +... 3ⁿ⁻¹)
or 8ⁿ - 3ⁿ = ( 5) (8ⁿ⁻¹ + 8ⁿ⁻² . 3 +... 3ⁿ⁻¹)
∴ 8ⁿ - 3ⁿ is divisible by 5
6. Prove that n⁵ - n is divisible by 5
n⁵ - n = n(n-1)(n+1)(n² + 1)
If the integer n terminates with one of the digits 0, 1, 4, 5, 6, or 9 then one of the first three
is divisible by 5
If n ends in one of the digits 2, 3, 7 or 8 then n² ends in 4 or 9, and in this event n² + 1 is divisible by 5
7. Prove that n⁷ - n is divisible by 7
8. Prove that n¹¹ - n is divisible by 11
9. Prove that n¹³ - n is divisible by 13
10. Prove