| Stamp issued on Dec 22, 1962, 75th birthday |
Carl Friedrich Gauss once said "Mathematics is the queen of the sciences and number theory is the queen of mathematics". In the field of Number Theory (the study of numbers and their properties), Ramanujan is one of those rare gems that continues to dazzle and inspire generations of mathematicians to this day.
The best biographical account on Ramanujan is SR Ranganathan's book.
In terms of understanding Ramanujan's work, prerequisites are undergrad-level knowledge of Number Theory and Complex Analysis.
This post is my effort to understand Ramanujan's work and his remarkable contributions. Having said that, to unravel the mathematics of Ramanujan is an impossible task for one life term, but hopefully I'll be able explore some facets of his life and work.
Srinivasa Ramanujan*
1. An intensely religious devout Hindu who had visions of mathematics.2. At age of twelve, Ramanujan borrowed a copy of the second part of S.L Loney's Plane Trigonometry (1893) and worked all the problems in it!
3. A book that transformed him, at age of fifteen, is GS Carr's "Synopsis of Elementary Results in Pure Mathematics". The Carr's book has about approximately 5000 formulas and theorems.
4. He was inspired by the goddess Sri Lakshmi Namagiri (generally know as goddess Lakshmi). Goddess Namagiri was their family deity and he was her ardent devotee.
5. A man who (twice) flunked out of college because of his single-minded devotion to mathematics
6. A man who accepted an incredible invitation from British mathematician Prof. G.H. Hardy to visit Trinity College, Cambridge, England (1913).
7. He soon became famous for the papers he published in England, some coauthored with Hardy. One of his most important papers is [3].
8. A man with ideas which surprised the accumulated wisdom of the worlds leading mathematicians
9. A man who had an intuition for numbers.
10. A man whose conjectures and assertions have led to the creation of fields of study.
11. A man who tragically passed away at the age of 32.
"Every positive integer is one of Ramanujan's personal friends" - J.E. Littlewood
I beg to introduce myself to you as a clerk
"Ramanujan used to say that the goddess of Namakkal inspired him with the formulae in dreams, It is remarkable fact that frequently, on rising from bed, he would note down results and rapidly verify them, though he was not always able to supply rigorous proof" - P.V. Seshu Ayar and R. Ramachandra Rao
*Note: In his Hindu horoscope Ramanujan is actually spelled as "Ramanujam".
First letter to Prof. G.H. Hardy (dated 16 Jan, 1913)
I have no University education
...I have not trodden through the conventional regular course.. but I am striking out a new path for myself
...and the results I get are termed by local mathematicians as "startling"
After the above introduction Ramanujan included formulas and theorems for the about next ten pages and contained 120 theorems !
Hardy's reaction to the first letter
After losing sleep the day he received the letter, Hardy invited his colleague Littlewood to have a look at Ramanujan's letter. After three hours of study, Hardy concluded this was work of a genius!"[These formulas ] defeated me completely. I had never seen anything in the least like this before. A single look at them is enough to show they could only be written down by a mathematician of the highest class. They must be true because no one would have the imagination to invent them. "
Hardy and Littlewood were excited the next day because they believed they had found a second Newton!
Example of a formula Ramanujan attached in his first letter to Hardy
each alternating term is given by
and their sum suddenly turns out to be equal to
National Mathematics Day
Ramanujan's birthday (Dec 22nd) is celebrated as National Mathematics Day in India. |
| Issued in 2012 |
1. Prime Numbers
2. Hypergeometric Series
3. Elliptic Functions
4. Partitions
5. Probabilistic Number Theory (is a subfield of number theory, which explicitly uses probability to answer questions of number theory.)
seven of the thirty papers were coauthored with Hardy.
Three papers that shaped the course of 20th century mathematics
1. G.H Hardy and S. Ramanujan, The normal number of prime factors of a number n (1917)
2. G.H Hardy and S. Ramanujan, Asymptotic formulae in combinatory analysis (1918)
3. S Ramanujan, On certain arithmetical functions (1916)
Ramanujan Notebooks
1. Much of Ramanujan's work was not published during his lifetime, but was summarized in his Notebooks.
2. Ramanujan would work on a slate and write the final formula in a notebook. He had a permanent scar on his elbow repeatedly using it to erase the slate.
3. From the age of 14 Ramanujan wrote down in 3 notebooks (in addition to the Lost Notebook) these are know as "frayed notebooks".
4. These notebooks contain over 4000 formulae.The first notebook has 351 pages with 16 somewhat organized chapters and some unorganized material. The second notebook has 256 pages in 21 chapters and 100 unorganized pages, with the third notebook containing 33 unorganized pages.
 |
| S. Narayana Aiyer holding Ramanujan's original slate |
The Lost Notebook
After Ramanujan passed away, his notebooks where passed on eventually to Hardy. Some time between 1934 and 1947, Hardy probably passed the notebook on to G. N. Watson, who with B. M. Wilson started on the project of editing Ramanujan's notebooks. G.N. Watson died in February 1965.
A decade later, in the Spring of 1976, when Prof. George E. Andrews of the Pennsylvania State University was going through the estate of Watson, he discovered a box of papers. These are now referred to as the contents of the 'Lost' notebook of Ramanujan.
The discovery of the `Lost' Notebook contributed to a resurgence of interest in the life and work of Ramanujan. This `Lost' Notebook contained some 600 theorems on what Ramanujan called as `mock' theta functions. These are results he noted on about 100 loose sheets of paper, during the last year of his life, after his return to India, in March 1919.
Ramanujan awarded FRS (Fellow of Royal Society)
Ramanujan became a FRS in Oct 10, 1918, becoming the second Indian to do so and he was one of the youngest Fellows in the history of the Royal Society. He was elected "for his investigation in Elliptic functions and the Theory of Numbers."

The certificate of Ramanujan's nomination to become a Fellow of the Royal Society. Click here to see a larger image.
Mahalanobis and Ramanujan would often used to go out for long walks on Sunday mornings. During these walks their discussions ranged over a wide variety of subjects. Quotes from Prof. P.C. Mahalanobis on Ramanujan.
"Left to himself, he would often speak of certain philosophical questions. He was eager to work out a theory of reality which would be based on the fundamental concepts of “zero”, “infinity” and the set of finite numbers."
"I used to follow in a general way but I never clearly understood what he had in mind. He sometimes spoke of “zero” as the symbol of the absolute (Nirguna-Brahmam) of the extreme monistic school of Hindu philosophy, that is, the reality to which no qualities can be attributed, which cannot be defined or described by words, and which is completely beyond the reach of the human mind."
“Ramanujan had a somewhat shy and quiet disposition, a dignified bearing, and pleasant manners. He would listen carefully to that other people were saying but would usually remain silent. If he was asked any question, or on rare occasions, if he joined in any general conversation, he would speak frankly, but briefly."
"His bright eyes and gentle face with a friendly smile are still vivid in my mind.”
Ramanujan arrived in Cambridge in April 1914. There he had 3 years of uninterrupted activity, doing much of his best work in collaboration with Hardy. Hardy to wrote to Madras University saying "He will return to India with a scientific standing and reputation such as no Indian enjoyed before". The theory of partitions is one of the outstanding examples of the success of Hardy-Ramanujan collaboration.
The function p(n) is the number of ways of partitioning n. For example, 4 can be partitioned in 5 possible ways 1+1+1+1, 1+1+2, 2+2, 1+3, and 4. Denoted by p(4) = 5.
p(n) = #{ways of representing n as a sum of natural numbers }.
p(7) = 15
where τ = 2π
Note - An asymptotic formula gives an estimates of the number of numbers below some arbitrarily large integer n that have a certain desired property. The farther out you go in the integers - in other words, the larger you choose n - the more accurate the estimate becomes as a percentage of the true value.
The Ramanujan Partition Congruences
Ramanujan spotted numbers ending in 4 or 9 have a partition number divisible by 5, and he found similar rules for partition numbers divisible by 7 and 11.
Let n be a non-negative integer and let p(n) denote the number of partitions of n (that is, the number of ways to write n as a sum of positive integers).
As noticed by Ramanujan, p(n) satisfies the congruence relations:
&space;\equiv&space;0&space;\:&space;(&space;mod&space;\:&space;5)) e.g. p(9) = 30
e.g. p(9) = 30
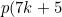&space;\equiv&space;0&space;\:&space;(&space;mod&space;\:&space;7))
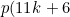&space;\equiv&space;0&space;\:&space;(&space;mod&space;\:&space;11))
&space;\leq&space;n&space;=&space;number&space;\:&space;of&space;\:&space;primes&space;\:&space;\leq&space;n) (n= 1, 2, 3, ..)
(n= 1, 2, 3, ..)
Primes = { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67,... }
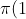&space;=&space;0)
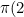&space;=&space;1)
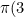&space;=&space;2)
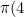&space;=&space;2)
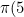&space;=&space;3)
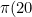&space;=&space;8&space;\:&space;\left\{&space;2,&space;3,&space;5,&space;7,&space;11,&space;13,&space;17,&space;19\right&space;\})
OEIS series link
Ramanujan primes is a prime number that satisfies a result proven by Ramanujan. It relates to the prime counting function. Ramanujan Prime is denoted by Rn, where n is serial number of that Ramanujan Prime.
Ramanujan prime Rn satisfies the following result proved by Ramanujan:
Some Examples:
Example 1
Example 2
8 -4 x ≥ 2 , 4 x≥ 3
Background - Gauss studied the cube of the Euler 𝜙-function.
^3&space;=&space;(1-x)^3\,\,&space;(1-x^2)^3\,\,&space;(1-x^3)^3\,\,&space;(1-x^3)^4....&space;\\*\\*&space;\:&space;\:&space;\:&space;\:\:&space;\:&space;\:&space;\:&space;=&space;1&space;-&space;3x&space;+&space;5x^3&space;-7x^6&space;+&space;9&space;x^{10}&space;-&space;11&space;x^{15})
The powers are 1, 3, 5, 10, 15, are exactly triangular numbers !
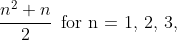
tau-function!
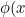^{24}&space;=&space;1&space;-24x&space;+&space;252x^2&space;-&space;1472x^3&space;+&space;4830x^4&space;-&space;6048&space;x^5+...)
The coefficients of powers of x is know as the τ-function or the Ramanujan's τ tau function
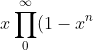^{24}&space;=&space;\sum_{n=1}^{\infty}&space;\tau&space;(n)&space;x^n)
τ(2) = -24, τ(3) = 252
OEIS series link
It may seem seem at first sight that the definition
of τ(n) is artificial. However, it is one of the most
important arithmetical functions in number theory
and arises in many contexts, in particular, in the
theory of modular forms.
Properties of τ function
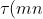&space;=&space;\tau(m)&space;\tau(n)&space;\:&space;\:&space;where&space;\:\:&space;(m,n)&space;=&space;1)
τ(6) = τ(2) τ(3) = -6048
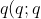^{24}_\infty&space;=&space;\sum_{n=1}^{\infty}&space;\tau(n)q^n)
π Approximation
How could anyone come-up with a formula like this ?! perhaps, the divine intuition of goddess Namagiri !
Computer scientists have exploited this series to calculate the value of π to million digits; each successive term in the series adds roughly eight more digits.
Alex Bellos ('Adventures in Numberland' fame) calls this formula "industrial-strength pi-making machine". :)
Ramanujan Infinite Series Sum
The sheer genius of Ramanujan in number theory is shown in this infinite series summation. When he showed that

Proof provided by Ramanujan



Some herald this is as "one of the most remarkable formulae in science".
Checkout the Numberphile Video which brought this equation to the popular media ... An NY Times article commented that "After watching the video myself, I checked to make sure I still had my wallet and my watch" :)
Math Plus article points to the flaw or the trick in this calc. Also, checkout Mathologer's rebuttal.

Ramanujan arrived at this as follows:
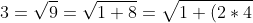}&space;=&space;\sqrt&space;{1+(2*&space;\sqrt{16})})
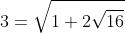}&space;=&space;\sqrt&space;{1+&space;2&space;\sqrt{(1&space;+3*5)})}&space;=&space;\sqrt&space;{1+&space;2&space;\sqrt{1&space;+3\sqrt{25}}})

A similar series can be constructed for number 4
Ramanujan provided the continued fraction for the Golden ratio ( ) which plays a beautiful role in math, culture and art.
) which plays a beautiful role in math, culture and art.
}{2}&space;=&space;1+\frac{1}{1+\frac{1}{1+\frac{1}{..}}})
this continued fraction can be solved by as roots of the equation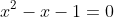
An actual question that people were thinking about is; can we generalize the
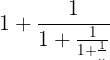
to
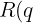&space;=&space;1+\frac{q}{1+\frac{q^2}{1+\frac{q^3}{..}}})
that is, given a power series R and a variable q, is there a theory for its special values ? So, if we substitute q =1, we get the equation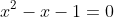 . If we substitute other values of q can we evaluate the function R(q)
. If we substitute other values of q can we evaluate the function R(q)
Ramanujan in his initial letter to Proof GH Hardy, had substituted the values of to provide the below two identities:
to provide the below two identities:
&space;e^\frac{2\pi}{5})
&space;e^\frac{\pi}{5})
Ramanujan ended his initial letter with the below equation and mentioned the series could be solved for any rational value of 'n' !
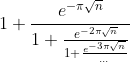
An other contiued function, that this is regarded as one of Ramanujan's most beautiful formula, a true product of the mathematical art is the one below... It unexpectedly relates an infinite series and an infinite continued fraction.
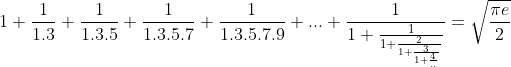
Rogers-Ramanujan Identities
"It would be difficult to find more beautiful formulae than the ‘Rogers–Ramanujan’ identities..” G.H. Hardy
The most interesting continued fractions in mathematics, is the Rogers-Ramanujan identities:
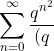_n}&space;=&space;\prod_{j=0}^{\infty}\frac{1}{(1-q^{5j+1})&space;(1-q^{5j+4})}&space;\\*&space;\\*&space;\\*\sum_{n=0}^{\infty}\frac{q^{n^{n+1}}}{(q)_n}&space;=\prod_{j=0}^{\infty}\frac{1}{(1-q^{5j+2})&space;(1-q^{5j+3})})
where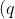_n&space;=&space;(1-q)&space;(1-q^2)...(1-q^n)&space;\:&space;\:&space;\textup{\mathrm{for}}&space;\:&space;\:&space;n&space;>0&space;\:&space;\:&space;and\:&space;\:&space;(q)_0=1)
So, what does the Rogers-Ramanujan identities mean ? Basically, they give us two different expressions for the same function, a function in q. Although this equality between sums and products expressed by these identities may appear rather obscure, the implications of this identity is significant
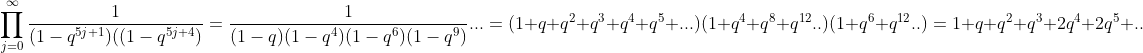
Expanding the left-hand side of the Rogers-Ramanujan function
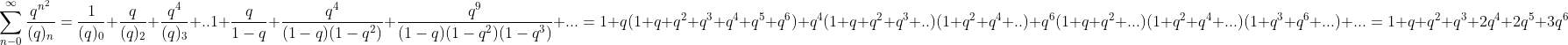
Both sides of the Rogers-Ramanujan equation yield the same power series.
These identities (written in generating function form) are typically of the form ''product side'' equals ''sum side'', with the product side enumerating partitions obeying certain congruence conditions and the sum side obeying certain initial conditions and difference conditions (along with possibly other restrictions)
Partition Interpretation of Rogers-Ramanujan
A partition of a positive integer is a way of writing it as a weakly decreasing sum of smaller integers.
The product side is the generating function of partitions with parts congruent 1 or 4 modulo 5.
Example: The coefficient of is 3 since there are
three partitions of 6 with parts congruent to 1 or 4
modulo 5:
(1, 1, 1, 1, 1, 1), (4, 1, 1) and (6).
is 3 since there are
three partitions of 6 with parts congruent to 1 or 4
modulo 5:
(1, 1, 1, 1, 1, 1), (4, 1, 1) and (6).
Rogers-Ramanujan Hard Hexagonal Model Ramanujan's mathematics was extensively used by Baxter, the well-known physicist from Australia. He used the famous Rogers-Ramanujan identities in what is called the hard hexagon model to describe the molecular structure of a thin film.
In his famous last letter aka death-bed letter, Ramanujan “defined” the notion of a mock theta function and offered some examples of functions he believed satisfied his definition.
Ramanujan listed 17 examples of these functions, but didn’t explain what they had in common. The question remained open for more than eight decades, until Sander Zwegers, then a graduate student of Zagier’s and now a professor at the University of Cologne in Germany, figured out in 2002 that they are all examples of what came to be known as mock modular forms.
Technically, modular forms are holomorphic functions on the upper half complex plane. They are defined on lattices in the complex plane.
Ramanujan motivated the mock theta functions by first describing briefly two “genuine” theta functions. The first example is the q-series for the partition function p(n):

A q-series is simply a power series in powers of q, whose coefficients usually count something of combinatorial interest. Here p(n) counts the number of ways of expressing n as a sum of positive integers, repetition allowed and not counting order. For example, p(6) = 11, since
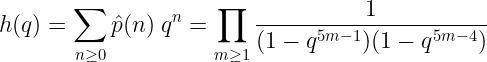
where now ˆp(n) equals the number of partitions into parts of the forms 5m − 1 and 5m − 4. A mock theta function, as conceived by Ramanujan, is a special kind of q-series that mimics two properties of g(q) and h(q). The first is that they can be expressed in Eulerian form: [TBC]
**************
"Srinivasa Ramanujan was a mathematician so great that his name transcends jealousies, the one superlatively great mathematician whom India has produced in a thousand years"
Ramanujan's legacy is rich and enduring. His influence continues to be felt across number of areas in Mathematics such as Ramanujan graphs, proof of Fermat's last theorem, probabilistic number theory to Physics - black holes and string theory (a prime candidate for a "theory of everything" uniting the disparate strands of modern physics). His conjectures continue to capture the minds of mathematicians and physicists to this day. And there were many others who were inspired by the genius of Ramanujan - Freeman Dyson, Bruce Brendt, Atle Selberg, Hans Rademacher, ...
So, the mystery of how Ramanujan actually obtained his prescient insights about number and equations remain even now.
Finally, to quote Ken Ono, "Every once in a while someone comes along in science and propels humanity forward Einstein, Newton and even Ramanujan belongs to that league!"
References
0. Number Theory in The Spirit Of Ramanujan - Bruce C. Brendt
1. The Institute of Mathematical Sciences - Ramanujan Website
2. Documentary on Ramanujan
3. Gems of Ramanujan and their Lasting Impact on Mathematics - Ken Ono
4. The On-Line Encyclopedia of Integer Sequences
5. Mock theta functions - Ken Ono
6. Biography - Srinivasa Ramanujan
7. Living with Ramanujan for 40 years - Bruce C. Brendt
8. Tales of Mathematicians and Physicists - Simon Gindikin
9. Ramanujan - The Man & The Mathematician - S.R Rangathan
10. Srinivasa Ramanujan: in celebration of the centenary of his election as FRS
11. Rediscovering Ramanujan - Interview with Prof. Bruce C. Berndt.
Some Papers
[0] S Ramanujan, Some properties of Bernoulli's numbers, J. Indian Math. Soc., (1911)
[1] S Ramanujan, Modular equations and approximations to π, 1914
[2] S Ramanujan, Highly composite numbers, 1914
[3] S Ramanujan, On certain arithmetical functions, 1916
[4] S Ramanujan, On certain trignometrical sums and their applications in the they of numbers, 1917
[5] G.H Hardy and S. Ramanujan, The normal number of prime factors of a number n, 1917
[6] G.H Hardy and S. Ramanujan, Asymptotic formulae in combinatory analysis, 1918
Background Materials
a. Elementary Number Theory - David M. Burton
b. Complex Analysis - Elias M. Stein & Rami Shakarchi
c. Visualizing the Riemann hypothesis and analytic continuation

The certificate of Ramanujan's nomination to become a Fellow of the Royal Society. Click here to see a larger image.
Prof. P.C. Mahalanobis on Ramanujan:
Mahalanobis and Ramanujan would often used to go out for long walks on Sunday mornings. During these walks their discussions ranged over a wide variety of subjects. Quotes from Prof. P.C. Mahalanobis on Ramanujan.
"Left to himself, he would often speak of certain philosophical questions. He was eager to work out a theory of reality which would be based on the fundamental concepts of “zero”, “infinity” and the set of finite numbers."
"I used to follow in a general way but I never clearly understood what he had in mind. He sometimes spoke of “zero” as the symbol of the absolute (Nirguna-Brahmam) of the extreme monistic school of Hindu philosophy, that is, the reality to which no qualities can be attributed, which cannot be defined or described by words, and which is completely beyond the reach of the human mind."
“Ramanujan had a somewhat shy and quiet disposition, a dignified bearing, and pleasant manners. He would listen carefully to that other people were saying but would usually remain silent. If he was asked any question, or on rare occasions, if he joined in any general conversation, he would speak frankly, but briefly."
"His bright eyes and gentle face with a friendly smile are still vivid in my mind.”
Collaboration with Prof. G.H. Hardy on the famous Partition Formula
"..my association with him was the one romantic incident in my life" - G.H. Hardy
Ramanujan arrived in Cambridge in April 1914. There he had 3 years of uninterrupted activity, doing much of his best work in collaboration with Hardy. Hardy to wrote to Madras University saying "He will return to India with a scientific standing and reputation such as no Indian enjoyed before". The theory of partitions is one of the outstanding examples of the success of Hardy-Ramanujan collaboration.
The function p(n) is the number of ways of partitioning n. For example, 4 can be partitioned in 5 possible ways 1+1+1+1, 1+1+2, 2+2, 1+3, and 4. Denoted by p(4) = 5.
The possible partitions rapidly increase -
p(n) = #{ways of representing n as a sum of natural numbers }.
p(7) = 15
p(10) = 42
p(20) = 627
p(30) = 5,604
p(40) = 37,338
p(50) = 204,226
OEIS series link
Ramanujan and Hardy's asymptotic formula for p(n)
&space;\sim&space;\frac{1}{4n\sqrt{3}}&space;e(^{\tau\sqrt{n/6}}))
p(20) = 627
p(30) = 5,604
p(40) = 37,338
p(50) = 204,226
OEIS series link
Ramanujan and Hardy's asymptotic formula for p(n)
where τ = 2π
Hardy Ramanujan proof for p(n) asymptotic formula is considered as one of masterpieces in Number Theory.
Note - An asymptotic formula gives an estimates of the number of numbers below some arbitrarily large integer n that have a certain desired property. The farther out you go in the integers - in other words, the larger you choose n - the more accurate the estimate becomes as a percentage of the true value.
The Ramanujan Partition Congruences
Ramanujan spotted numbers ending in 4 or 9 have a partition number divisible by 5, and he found similar rules for partition numbers divisible by 7 and 11.
Let n be a non-negative integer and let p(n) denote the number of partitions of n (that is, the number of ways to write n as a sum of positive integers).
As noticed by Ramanujan, p(n) satisfies the congruence relations:
Ramanujan Primes
The prime counting function shows the number of primes less than or equal to n. It is denoted by π(n).Primes = { 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67,... }
OEIS series link
Ramanujan primes is a prime number that satisfies a result proven by Ramanujan. It relates to the prime counting function. Ramanujan Prime is denoted by Rn, where n is serial number of that Ramanujan Prime.
Ramanujan prime Rn satisfies the following result proved by Ramanujan:
Rn Ramanujan Primes = {2, 11, 17, 29, 41, 47, 59, 67, 71, 97, 101, 107, 127, 149, 151, 167, 179, 181, 227, 229, 233, 239, 241, 263, 269, 281, 307, 311, 347, 349, 367, 373, 401, 409, 419, 431, 433, ...}
Some Examples:
Example 1
R2 = 11, take x ≥ 11, say 13
π(x)−π(x/2)≥n
π(13)−π(13/2)≥2
6 -3 x ≥ 2 , 3 x≥ 2
Example 2
R3 = 17, take x ≥ 17, say x = 20
π(x)−π(x/2)≥n
π(20)−π(20/2)≥3
8 -4 x ≥ 2 , 4 x≥ 3
With the help of Ramanujan prime we can find the minimum number of prime number that exist
between a number and its half.
Ramanujan τ (tau) Function
In his remarkable paper [3] Ramanujan introduced the τ functionBackground - Gauss studied the cube of the Euler 𝜙-function.
The powers are 1, 3, 5, 10, 15, are exactly triangular numbers !
tau-function!
The coefficients of powers of x is know as the τ-function or the Ramanujan's τ tau function
τ(2) = -24, τ(3) = 252
OEIS series link
It may seem seem at first sight that the definition
of τ(n) is artificial. However, it is one of the most
important arithmetical functions in number theory
and arises in many contexts, in particular, in the
theory of modular forms.
Properties of τ function
τ(6) = τ(2) τ(3) = -6048
π Approximation
Ramanujan in one of papers ([1], Modular equations and approximations to π) gave 19 infinite series representation to π! Ramanujan's formula for π is still used in algorithms in electromagnetic signals,
satellites and GPS tracking.
satellites and GPS tracking.

Computer scientists have exploited this series to calculate the value of π to million digits; each successive term in the series adds roughly eight more digits.
Alex Bellos ('Adventures in Numberland' fame) calls this formula "industrial-strength pi-making machine". :)
Ramanujan Infinite Series Sum
The sheer genius of Ramanujan in number theory is shown in this infinite series summation. When he showed that
Proof provided by Ramanujan


Some herald this is as "one of the most remarkable formulae in science".
Checkout the Numberphile Video which brought this equation to the popular media ... An NY Times article commented that "After watching the video myself, I checked to make sure I still had my wallet and my watch" :)
Math Plus article points to the flaw or the trick in this calc. Also, checkout Mathologer's rebuttal.
Nested Radicals and Continued Fractions
Ramanujan developed several formulae that allowed him to calculate nested radicals such asRamanujan arrived at this as follows:
A similar series can be constructed for number 4
Ramanujan provided the continued fraction for the Golden ratio (
this continued fraction can be solved by as roots of the equation
An actual question that people were thinking about is; can we generalize the
to
that is, given a power series R and a variable q, is there a theory for its special values ? So, if we substitute q =1, we get the equation
Ramanujan in his initial letter to Proof GH Hardy, had substituted the values of
Ramanujan ended his initial letter with the below equation and mentioned the series could be solved for any rational value of 'n' !
An other contiued function, that this is regarded as one of Ramanujan's most beautiful formula, a true product of the mathematical art is the one below... It unexpectedly relates an infinite series and an infinite continued fraction.
Rogers-Ramanujan Identities
"It would be difficult to find more beautiful formulae than the ‘Rogers–Ramanujan’ identities..” G.H. Hardy
The most interesting continued fractions in mathematics, is the Rogers-Ramanujan identities:
where
So, what does the Rogers-Ramanujan identities mean ? Basically, they give us two different expressions for the same function, a function in q. Although this equality between sums and products expressed by these identities may appear rather obscure, the implications of this identity is significant
Expanding the left-hand side of the Rogers-Ramanujan function
Both sides of the Rogers-Ramanujan equation yield the same power series.
These identities (written in generating function form) are typically of the form ''product side'' equals ''sum side'', with the product side enumerating partitions obeying certain congruence conditions and the sum side obeying certain initial conditions and difference conditions (along with possibly other restrictions)
Partition Interpretation of Rogers-Ramanujan
A partition of a positive integer is a way of writing it as a weakly decreasing sum of smaller integers.
The product side is the generating function of partitions with parts congruent 1 or 4 modulo 5.
Example: The coefficient of
Rogers-Ramanujan Hard Hexagonal Model Ramanujan's mathematics was extensively used by Baxter, the well-known physicist from Australia. He used the famous Rogers-Ramanujan identities in what is called the hard hexagon model to describe the molecular structure of a thin film.
Fermat's Theorem and Near Misses
Fermat's lost theorem looks for numbers which satisfy this equation 
Ramanujan is his famous lost notebook has pinned down infinite number of near misses, numbers of the form
 example
example 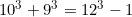
which almost satisfies the Fermat's last theorem. Was Ramanujan in search of a proof for Fermat's lost theorem ?
Ramanujan is his famous lost notebook has pinned down infinite number of near misses, numbers of the form
which almost satisfies the Fermat's last theorem. Was Ramanujan in search of a proof for Fermat's lost theorem ?
Mock Theta Functions
In his famous last letter aka death-bed letter, Ramanujan “defined” the notion of a mock theta function and offered some examples of functions he believed satisfied his definition.
Ramanujan listed 17 examples of these functions, but didn’t explain what they had in common. The question remained open for more than eight decades, until Sander Zwegers, then a graduate student of Zagier’s and now a professor at the University of Cologne in Germany, figured out in 2002 that they are all examples of what came to be known as mock modular forms.
Technically, modular forms are holomorphic functions on the upper half complex plane. They are defined on lattices in the complex plane.
Ramanujan motivated the mock theta functions by first describing briefly two “genuine” theta functions. The first example is the q-series for the partition function p(n):
A q-series is simply a power series in powers of q, whose coefficients usually count something of combinatorial interest. Here p(n) counts the number of ways of expressing n as a sum of positive integers, repetition allowed and not counting order. For example, p(6) = 11, since
where now ˆp(n) equals the number of partitions into parts of the forms 5m − 1 and 5m − 4. A mock theta function, as conceived by Ramanujan, is a special kind of q-series that mimics two properties of g(q) and h(q). The first is that they can be expressed in Eulerian form: [TBC]
**************
Legacy of Ramanujan
“I have never met his equal, and I can compare him only with Euler or Jacobi....with his memory, his patience and his power of calculation, he combined a power of generalisation, a feeling for form, a capacity for rapid modification of his hypothesis, that were often really startling, and made him, in his own peculiar field, without a rival in his day.” G.H. Hardy
"Srinivasa Ramanujan was a mathematician so great that his name transcends jealousies, the one superlatively great mathematician whom India has produced in a thousand years"
The Mystery Remains
Professor Bruce Berndt spent 40+ years studying Ramanujan's letters and notebooks - including a "lost notebook", trying to supply proofs for mathematical results Ramanujan stated as facts. And he remarked
"At times I have no idea where these formulae are coming from. There are times I would think of a formula over for about six months or even a year, not getting anywhere. Even now there are times when we wonder how Ramanujan was ever led to the formulae. There has to be some chain of reasoning to lead him to think that there might be a theorem there. But often this is missing. To begin with, the formulae look strange but over time we understand where they fit in and how important they are than they were previously thought to be."
So, the mystery of how Ramanujan actually obtained his prescient insights about number and equations remain even now.
Finally, to quote Ken Ono, "Every once in a while someone comes along in science and propels humanity forward Einstein, Newton and even Ramanujan belongs to that league!"
References
0. Number Theory in The Spirit Of Ramanujan - Bruce C. Brendt
1. The Institute of Mathematical Sciences - Ramanujan Website
2. Documentary on Ramanujan
3. Gems of Ramanujan and their Lasting Impact on Mathematics - Ken Ono
4. The On-Line Encyclopedia of Integer Sequences
5. Mock theta functions - Ken Ono
6. Biography - Srinivasa Ramanujan
7. Living with Ramanujan for 40 years - Bruce C. Brendt
8. Tales of Mathematicians and Physicists - Simon Gindikin
9. Ramanujan - The Man & The Mathematician - S.R Rangathan
10. Srinivasa Ramanujan: in celebration of the centenary of his election as FRS
11. Rediscovering Ramanujan - Interview with Prof. Bruce C. Berndt.
Some Papers
[0] S Ramanujan, Some properties of Bernoulli's numbers, J. Indian Math. Soc., (1911)
[1] S Ramanujan, Modular equations and approximations to π, 1914
[2] S Ramanujan, Highly composite numbers, 1914
[3] S Ramanujan, On certain arithmetical functions, 1916
[4] S Ramanujan, On certain trignometrical sums and their applications in the they of numbers, 1917
[5] G.H Hardy and S. Ramanujan, The normal number of prime factors of a number n, 1917
[6] G.H Hardy and S. Ramanujan, Asymptotic formulae in combinatory analysis, 1918
Background Materials
a. Elementary Number Theory - David M. Burton
b. Complex Analysis - Elias M. Stein & Rami Shakarchi
c. Visualizing the Riemann hypothesis and analytic continuation

