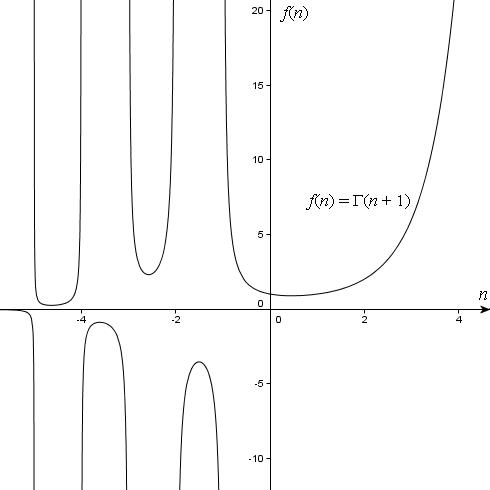Visions of Mathematics: Gamma Functions

Gamma function

Many important functions in applied sciences are defined via improper integrals. Maybe the most famous among them is the Gamma Function.

Represents the extension of the factorial function. Unlike more familiar functions such as polynomials or trigonometric functions, the gamma function is defined as the improper integral of another function.

The gamma function extends the factorial function to real numbers. Since factorial is only defined on non-negative integers, there are many ways you could define factorial that would agree on the integers and disagree elsewhere.

Gamma function as defined by Euler (Notes from Prof. V. Balakrishnan Lectures)

$\int_{0}^{\infty } dt \, t^n \,e ^-t = n!$ where n = 1, 2, 3...

We can use this definition to define 0!

$\int_{0}^{\infty } dt \, t^0 \,e ^-t = 0! \equiv 1$

To calculate factorials beyond a certain number we need a formula, which is given by

Stirling's Formula

$n! = n^n \; e ^-^n \sqrt{2 \pi n}$

Euler Gamma function

$\int_{0}^{\infty } dt \; t ^n^-^1 e ^-^t = \Gamma (n)$ (n = 1, 2, 3, ..)

When n is a complex number

$\Gamma (n) = \int_{0}^{\infty } dt \; z ^n^-^1 e ^-^t; Re \, z > 0$

$\Gamma (z) =\frac{1}{z} \int_{0}^{\infty } t^z \; e ^-^t$

$\Gamma (z)$ is a meromorphic function with simple poles for z = -n (n= 1, 2, 3, ...) and residue $\frac{(-1)^n}{n!}$

Functional Equation

$\Gamma (z+1) = z \, \Gamma (z)$

Definition of pi

$\Gamma (\frac{1}{2}) = \sqrt \pi$

Properties of Gamma Function

$1$

$\int_0^\infty x^{\alpha - 1} e^{-\lambda x} dx = \frac{\Gamma(\alpha)}{\lambda^{\alpha}}, \hspace{20pt} \textrm{for } \lambda > 0;$

$\Gamma(\alpha + 1) = \alpha \Gamma(\alpha);$

$\Gamma(n) = (n - 1)!, \textrm{ for } n = 1,2,3,\cdots ;$

$\Gamma(\frac{1}{2}) = \: (-\frac{1}{2})! \: = \sqrt{\pi}$

Calculate

1. Γ(5) = 4Γ(4) = 4 · 3Γ(3) = 4 · 3 · 2 · 1 · Γ(1) = 4! = 24.

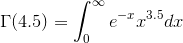
2. $\Gamma(4.5)=\int_0^{\infty}{e^{-x}}{x^{3.5}}dx$

Recall that 3! = 6 and 4! = 24. Our answer for Γ(4.5) = 3.5! has to be between these values.

Graphs involved with this integral

this is the graph of f(x) = e^−xx^3.5.

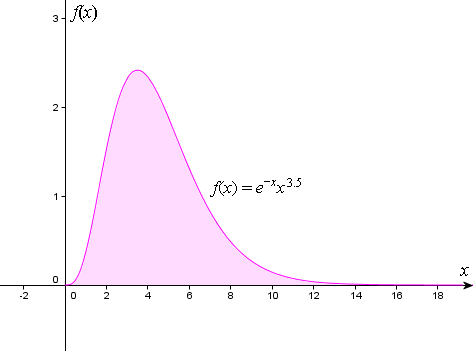
from the below curve Γ(4.5) = 11.6317

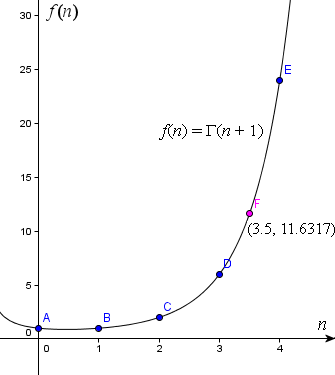
The Gamma function gives us values that are analogous to factorials of non-integer numbers.

Graph of f(n) = Γ(n + 1) for a greater range of real values of n.

observe there are some "holes" (discontinuities) in the graph for the negative integers.