Visions of Mathematics: Differential Equations

Two categories - ODE and PDE

1. First Order Ordinary Differential Equations

Standard form for a first-order differential equation is the unknown function f(x,y) is $y' = f(x,y)$ .

First order linear differential equation can be expressed in the form

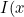$y' + p(x)y = q(x)$ has an integrating factor $I(x) = e^{\int p(x) dx}$

2. Second Order Ordinary Differential Equations
Homogeneous Linear Equations with Constant Coefficients

${y}'' + p{y}' + qy = 0$

The characteristic equation is

$\lambda ^2 + p\lambda + q = 0$

If $\lambda_1$ and $\lambda_2$ are distinct real roots of the characteristic equation, then the general solution is

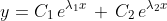
$y = C_1\, e^{\lambda_1x} \, + \, C_2\, e^{\lambda_2x}$

$C_1 \: and \: C_2$ are integration constants

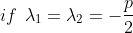
$if \: \: \lambda_1 = \lambda_2 = -\frac{p}{2}$

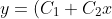$y = (C_1 + C_2x) e ^ {-\frac{p}{2}}$

Simple Pendulum

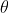$\frac{\mathrm{d^2}\theta }{\mathrm{d} t^2} + \frac{g}{L} \theta = 0$

Where $\theta$ is the angular displacement, L is the pendulum length, and g is the acceleration of gravity.

The general solution for small angles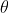 $\theta$ is

$\theta (t) = \theta_{max} \: sin\sqrt{\frac{g}{L}t} \:\:, the \: \: period \: \:T = 2 \pi\sqrt{\frac{L}{g}}$

RLC Circuit

3. Some Partial Differential Equations

The Laplace Equation
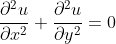
$\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0$

applies to potential energy function u (x,y) for a conservative force field in the xy-plane. Partial differential equations of this type are called elliptic

Analytic function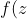 $f(z) = u (x,y) + i v (x,y)$ satisfy two-dimensional Laplace equation. Functions satisfying the Laplace equation are called harmonic functions.

The Heat Equation
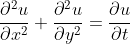
$\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = \frac{\partial u}{\partial t}$

applies to the temperature distribution u (x,y) in the xy-plane when heat is allowed to flow from warm areas to cool ones. The equations of this type are called parabolic

The Wave Equation
$\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = \frac{\partial^2 u}{\partial t^2}$

applies to the displacement u(x,y) of vibrating membranes and other wave functions. The equations of this type are called hyperbolic