Analytic Functions
Complex functions to which the concepts and structure of calculus can be applied are called analytic functions. The theory of analaytic functions is an extension of differential and integral calculus to realms of complex variables.
Differentiation of a Complex Function
If a complex function f(z) whoe derivative f'(z) exists at z0 and at every point in the neighborhood of z0, then the function is said to be analytic at z0. An analytic function is a function that is analytic in some regiion (domain) of the complex plane.
A function that is analytic in the whole complex plane is called an entire function.
A point at which an analytic function ceases to have a derivative is called a singular point.
Cauchy-Riemann Equations
Consider the function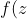&space;=&space;\frac{1}{z})
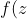&space;=&space;\frac{1}{z}&space;=&space;\frac{1}{x+iy}&space;=&space;\frac{1}{x+iy}&space;.&space;\frac{x-iy}{x-iy}&space;=&space;\frac{x-iy}{x^2+y^2}&space;=&space;\frac{x}{x^2+y^2}&space;-&space;\frac{iy}{x^2+y^2})
therefore
&space;=&space;\frac{x}{x^2+y^2})
&space;=&space;-&space;\frac{y}{x^2+y^2})
a)
&space;^2}&space;=&space;\frac{y^2&space;-&space;x^2}{(x^2+y^2)^2})
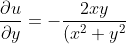&space;^2})
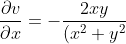&space;^2})
&space;^2}&space;+&space;\frac{2y^2}{(x^2+y^2)&space;^2}&space;=&space;\frac{y^2&space;-&space;x^2}{(x^2+y^2)&space;^2})
Clearly the Cauchy-Riemann equations are satisfied
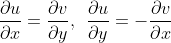
b)
The real part
^2}&space;+&space;\frac{(y^2&space;-&space;x^2)&space;(-2)&space;(2x)))}{(x^2+y^2)^3}&space;=&space;\frac{2x^3-&space;6xy^2}{(x^2+y^2)^3})
^2}&space;+&space;\frac{-2xy&space;\,&space;(-2)\,&space;(2y)}{(x^2+y^2)^3}&space;=&space;\frac{2x^3-&space;6xy^2}{(x^2+y^2)^3})
Thus the real part satifies the Laplace Equation
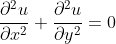
Furthermore,
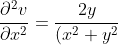^2}&space;+&space;\frac{(2xy)&space;(-2)&space;(2x)}{(x^2+y^2)^3}&space;=&space;\frac{2y^3-&space;6x^2y}{(x^2+y^2)^3})
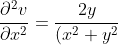^2}&space;+&space;\frac{(-x^2+y^2)&space;(-2)&space;(2y)}{(x^2+y^2)^3}&space;=&space;\frac{-2y^3+&space;6x^2y}{(x^2+y^2)^3})
The imaginary part also satifies the Laplace Equation

c) the equation
&space;=&space;\frac{x}{x^2+y^2}&space;=&space;k)
&space;^2&space;+&space;y^2&space;=&space;\frac{1}{4k^2})
which is a circle for any given constant k. Therefore u (x, y) = k is a family of circles centered at
with radius) with radius
with radius  . This family of circles is shown in figure as solid circles.
. This family of circles is shown in figure as solid circles.
&space;=&space;-&space;\frac{y}{x^2+y^2}&space;=&space;c) can be written as
can be written as
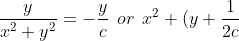^2&space;=&space;\frac{1}{4c^2})
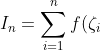&space;(z_i&space;-&space;z_{i-1})&space;=&space;\sum_{i=1}^{n}&space;f(\zeta_i)&space;\Delta&space;z_i)
&space;dz&space;=&space;\lim_{n&space;\rightarrow&space;\infty&space;\left&space;\:&space;\:&space;|\Delta&space;z_i&space;\right&space;|&space;\rightarrow&space;0}&space;\sum_{i=1}^{n}&space;f(\zeta_i)&space;\Delta&space;z_i)
&space;dz&space;=&space;\lim_{n&space;\rightarrow&space;\infty&space;\left&space;\:&space;\:&space;|\Delta&space;z_i&space;\right&space;|&space;\rightarrow&space;0}&space;\sum_{i=1}^{n}&space;f(\zeta_i)&space;\Delta&space;z_i)
since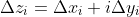
&space;dz&space;=&space;\int_{A&space;\:&space;\Gamma&space;}^{B}&space;(u+iv)(dx+idy)&space;=&space;\int_{A&space;\:&space;\Gamma&space;}^{B}&space;(u\:dx-v\:dy)&space;+&space;i\:(v\:dx+&space;u&space;\:&space;dy)&space;=&space;\int_{A&space;\:&space;\Gamma&space;}^{B}&space;(u\:dx-v\:dy)&space;+&space;i&space;\int_{A&space;\:&space;\Gamma&space;}^{B}&space;(v\:dx+&space;u&space;\:&space;dy))
Thus, the complex contour integral is expressed in terms of two line integrals.
Example -
![f(z) = z^2 = (x+iy)^2 = (x^2-y^2) + i2xy = u +iv \\*\\* \int_{A,\Gamma }^{B} f(z) dz = \int_{A,\Gamma }^{B} [(x^2-y^2) dx - 2 dxdxy] + i \int_{A,\Gamma }^{B} [2xydx + (x^2-y^2)dy] \\* \\*\\* \textup{(a) Along} \: \Gamma \_1, y = x^2, dy = 2x \: dx \\*\\*\\* \int_{A,\Gamma }^{B} f(z) dz = \int_{1}^{0}[(x^2 - x^4)dx - 2xx^22xdx] + i \int_{1}^{0} [2xx^2dx + (x^2 - x^4) 2xdx] \\*\\* =\int_{1}^{0} (x^2 - 5x^4) dx + i \int_{1}^{0} (4x^3 - 2x^5) dx = -\frac{2}{3} + \frac{2}{3}i](https://latex.codecogs.com/gif.latex?f(z)&space;=&space;z^2&space;=&space;(x+iy)^2&space;=&space;(x^2-y^2)&space;+&space;i2xy&space;=&space;u&space;+iv&space;\\*\\*&space;\int_{A,\Gamma&space;}^{B}&space;f(z)&space;dz&space;=&space;\int_{A,\Gamma&space;}^{B}&space;[(x^2-y^2)&space;dx&space;-&space;2&space;dxdxy]&space;+&space;i&space;\int_{A,\Gamma&space;}^{B}&space;[2xydx&space;+&space;(x^2-y^2)dy]&space;\\*&space;\\*\\*&space;\textup{(a)&space;Along}&space;\:&space;\Gamma&space;\_1,&space;y&space;=&space;x^2,&space;dy&space;=&space;2x&space;\:&space;dx&space;\\*\\*\\*&space;\int_{A,\Gamma&space;}^{B}&space;f(z)&space;dz&space;=&space;\int_{1}^{0}[(x^2&space;-&space;x^4)dx&space;-&space;2xx^22xdx]&space;+&space;i&space;\int_{1}^{0}&space;[2xx^2dx&space;+&space;(x^2&space;-&space;x^4)&space;2xdx]&space;\\*\\*&space;=\int_{1}^{0}&space;(x^2&space;-&space;5x^4)&space;dx&space;+&space;i&space;\int_{1}^{0}&space;(4x^3&space;-&space;2x^5)&space;dx&space;=&space;-\frac{2}{3}&space;+&space;\frac{2}{3}i)
Green's Theorem
There is an important relation that allows us to transform a line integral into an area integral for lines and areas in the xy plane. It is often referred to as Green's lemma
![\oint_C [P(x,y) dx + Q(x,y) dy] = \iint_R [\frac{\partial Q (x,y)}{\partial x} - \frac{\partial P (x,y)}{\partial x}] dx dy](https://latex.codecogs.com/gif.latex?\oint_C&space;[P(x,y)&space;dx&space;+&space;Q(x,y)&space;dy]&space;=&space;\iint_R&space;[\frac{\partial&space;Q&space;(x,y)}{\partial&space;x}&space;-&space;\frac{\partial&space;P&space;(x,y)}{\partial&space;x}]&space;dx&space;dy)

Cauchy-Goursat Theorem
An important theorem in complex integration is the following:
If C is a closed contour and f(z) is analytic on and inside C, then
\:&space;dz&space;=&space;0)
This is know as Cauch's theorem.
Fundamental Theorem of Calculus
If the closed contour Γ
Singularity - A point at which the function f fails to be analytic. Take the function f(z) = 1/z,the function is not anlaytic at zero, zero is a singularity.
at which the function f fails to be analytic. Take the function f(z) = 1/z,the function is not anlaytic at zero, zero is a singularity.
f (z) = Ln (z)
Isolated Singularity
Non-Isolated Singularity
Complex functions to which the concepts and structure of calculus can be applied are called analytic functions. The theory of analaytic functions is an extension of differential and integral calculus to realms of complex variables.
Differentiation of a Complex Function
If a complex function f(z) whoe derivative f'(z) exists at z0 and at every point in the neighborhood of z0, then the function is said to be analytic at z0. An analytic function is a function that is analytic in some regiion (domain) of the complex plane.
A function that is analytic in the whole complex plane is called an entire function.
A point at which an analytic function ceases to have a derivative is called a singular point.
Cauchy-Riemann Equations
Consider the function
therefore
a)
Clearly the Cauchy-Riemann equations are satisfied
b)
The real part
Thus the real part satifies the Laplace Equation
Furthermore,
The imaginary part also satifies the Laplace Equation
c) the equation
which is a circle for any given constant k. Therefore u (x, y) = k is a family of circles centered at
with radius
similary,
Therefore, Therefore v (x, y) = c is a family of circles of radius 1/2c , centered at (0,− 1/2c ).
They are shown as the dotted circles in the figure above. Those who are familiar with electrostatics will recognize that the curves in Fig. are electric field lines and equipotential lines of a line dipole.
Line Integral of a Complex Function
When a complex variable z moves in the two-dimensional complex plane, it traces out a curve.
 |
| The Riemann sum along the contour Γ which is subdivided into n segments |
since
Thus, the complex contour integral is expressed in terms of two line integrals.
Example -
Green's Theorem
There is an important relation that allows us to transform a line integral into an area integral for lines and areas in the xy plane. It is often referred to as Green's lemma

Cauchy-Goursat Theorem
An important theorem in complex integration is the following:
If C is a closed contour and f(z) is analytic on and inside C, then
This is know as Cauch's theorem.
Fundamental Theorem of Calculus
If the closed contour Γ
Singularity - A point
f (z) = Ln (z)
Isolated Singularity
Non-Isolated Singularity
